首页 | 目录 | 世界 | 学科 | 文科 | 科学 | 数学 | 物理 | 化学 | 医学 | 计算 | 软件 | 帮助 | 打赏
+ + + =

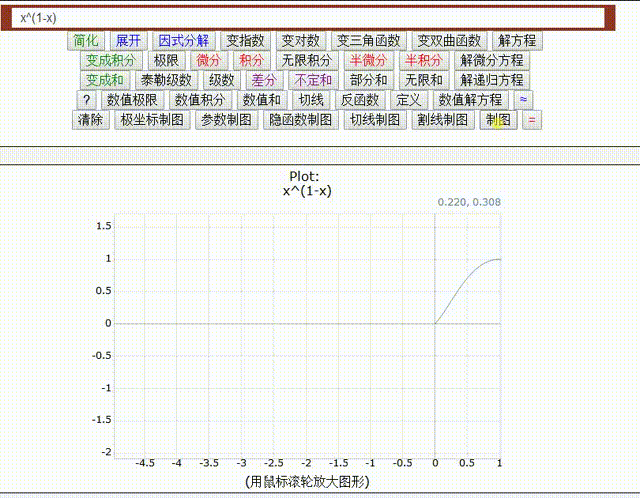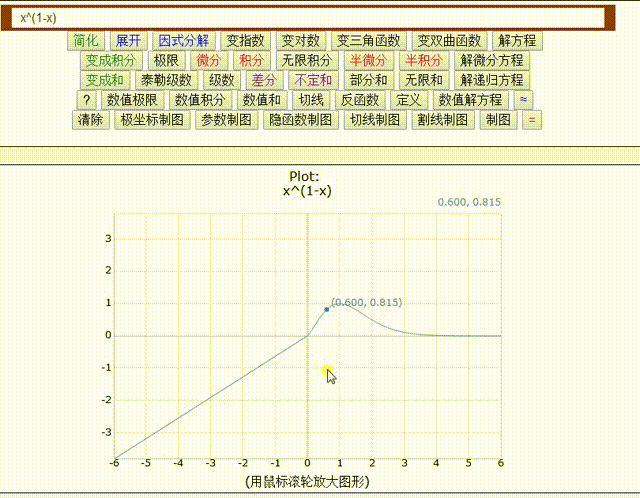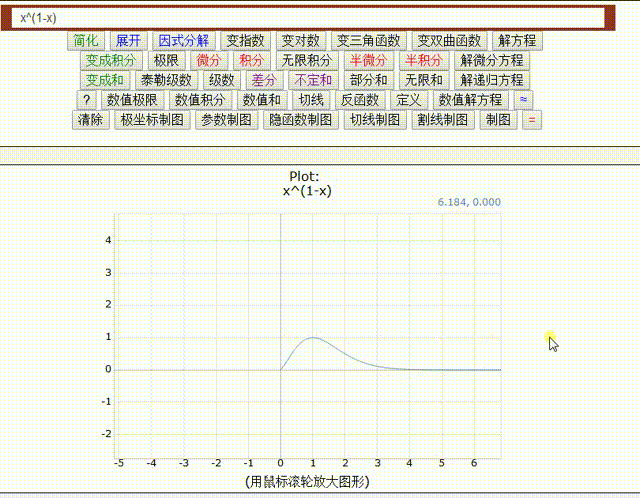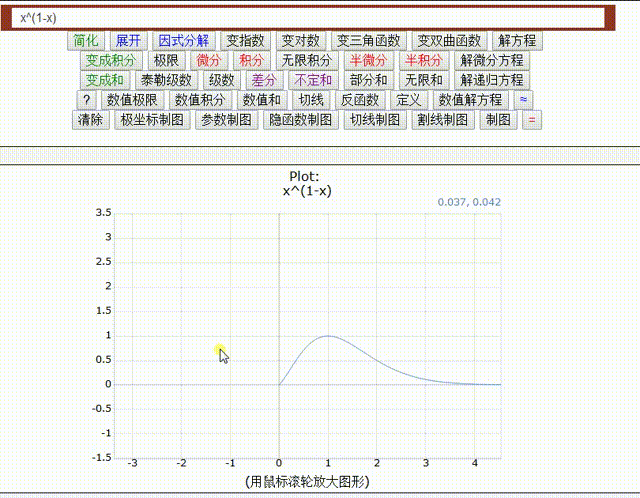
目 录

一、 高等数学 5
第一章 极限与连续 5
一、数列的极限：5
二、函数的极限：5
三、无穷小与无穷大：6
四、极限的运算法则：6
五、极限存在准则与两个重要极限：7
六、无穷小阶的比较：7
七、函数的连续性：7

第二章 导数与微分 8
一、函数的导数 8
二、微分：10

第三章 微分中值定理与导数应用 10
一、微分中值定理 10
二、洛比达法则：11
三、泰勒中值定理：12
四、函数的单调性与凹凸性：12
五、函数的极值及其求法13
六、曲率与弧微分 13

第四章 不定积分 14

第五章 定积分 15
一、定积分的概念 15
二、定积分的性质：15
三、微积分基本公式16
四、定积分的换元法与分部积分法 16
五、无穷区间上的反常积分 17

第六章 定积分的应用 18
一、元素法 18
二、平面图形的面积：19
三、体积 19
四、弧长 19

第八章 空间解析几何与向量代数 19
一、向量及其运算 19
二、曲面及其方程 20
三、空间曲线及其方程 21
四、平面及其方程 21
五、空间直线及其方程 21

第九章 多元函数微分法及其应用 22
一、平面点集 22
二、二元函数的极限及其连续性 23
三、偏导数 24
四、二元函数的微分 25
五、复合函数及隐函数求导 25
六、偏导数的几何应用 26
七、方向导数 27
八、二元函数的极值 28

第十章 重积分 29
一、二重积分 29
二、三重积分 30
三、重积分应用 30

第十一章 曲线积分与曲面积分 30
一、对长度曲线积分 30
二、对坐标的曲线积分 31
三、格林公式 32
四、对面积的曲面积分 33
五、对坐标的曲面积分 33
六、高斯公式 34
七、斯托克斯公式 35

第十二章 无穷级数 36
一、常数项级数 36
二、正数项级数 37
三、幂级数 38
四、泰勒级数 39
五、傅里叶级数 40

二、线性代数 41
第一章 行列式 41
一、行列式的定义 41
二、行列式的性质（包含其按行列展开） 41
三、克拉默法则（行列式的应用） 43

第二章 矩阵及其运算 43
一、矩阵的定义 43
二、矩阵的运算 44
三、方阵的逆 45
四、分块矩阵 47

第三章 矩阵的初等变换与线性方程组 48
一、矩阵的初等行变换 48
二、初等变换与矩阵运算的关系 49
三、矩阵的秩的概念 49
四、矩阵秩的相关性质 49
五、利用矩阵求解线性方程组与矩阵方程组（矩阵的应用1) 50

第四章 向量组的线性相关性 50
一、向量（组）的概念 50
二、向量组线性表示向量（组）（矩阵的应用 2-1) 50
三、向量组的线性相关性（矩阵的应用 2-2) 51
四、线性方程组解的结构 52
五、向量空间 53

第五章 相似矩阵及二次型 ................................................................................................. 53
一、向量的内积、长度及正交性 ................................................................................. 53
二、方阵的特征值与特征向量 ..................................................................................... 55
三、相似矩阵 ................................................................................................................. 56
四、对称矩阵的对角化 ................................................................................................. 56
五、二次型及其标准形 ................................................................................................. 57

三、概率论与数理统计 ................................................................................................... 58
第一章 概率论的基本概念 ................................................................................................ 58
一、随机试验、样本空间、随机事件 ......................................................................... 58
二、频率与概率（等可能概型的概率） ..................................................................... 58
三、条件概率（乘法公式、贝叶斯公式）及独立性 ................................................. 60

第二章 随机变量及其分布 ...................................................................................... 61
一、离散型随机变量及其分布律 ................................................................................. 61
二、随机变量的分布函数 ............................................................................................. 62
三、连续型随机变量及其概率密度 ............................................................................. 62
四、随机变量的函数的分布 ......................................................................................... 64

第三章 多维随机变量及其分布 ......................................................................................... 64
一、二维随机变量 ..................................................................................................... 64
二、边缘分布 ................................................................................................................. 65
三、条件分布 ................................................................................................................. 67
四、相互独立的随机变量 ............................................................................................. 67
五、两个随机变量的函数的分布 ................................................................................. 69

第四章 随机变量的数字特征 ........................................................................................... 70
一、数学期望 ........................................................................................................... 70
二、方差 .................................................................................................................. 71
三、协方差与相关系数 ................................................................................................. 72
四、矩、协方差矩阵 ..................................................................................................... 73

第五章 大数定律与中心极限定理 ................................................................................... 74
一、大数定律 ........................................................................................................ 74
二、中心极限定理 ......................................................................................................... 74

第六章 样本及抽样分布 ................................................................................................. 75

第七章 参数估计 ............................................................................................................... 79
一、点估计 ..................................................................................................................... 79
二、估计量的评选标准 ................................................................................................. 81
三、区间估计 ................................................................................................................. 82
※四、正态总体均值与方差的区间估计（教材表7-1） .......................................... 82

第八章 假设检验 ......................................................................................................... 83